文将帮助大家了解包括 PCB 上的走线在内的高频传输线中的损耗。还将研究这些损耗如何影响信号传播和数字信号的质量。

“传输线”这一术语用于区分高频信号传播的复杂行为与普通低频互连。在高频下，需要复杂的方程式来理解简单互连的行为。可以通过将线路划分为无限小长度的元素来等效传输线模型，其中每个元素本身被建模为电感器、电容器和两个电阻的组合网络。

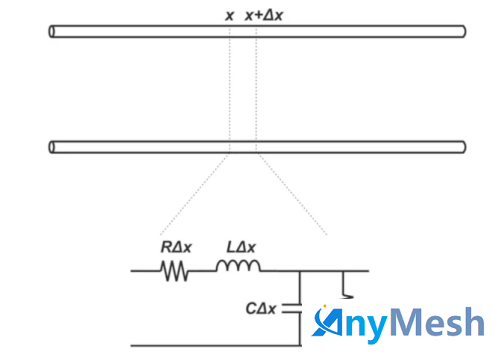
在许多应用中，无损(R=G=0)可以是一个合理的假设，因为在高频下，电感的电抗通常远大于串联电阻 R，而电容的电抗通常远小于分流电阻。尽管如此，在许多应用中，仍应考虑传输线的损耗。 

例如，在笔记本电脑或台式电脑等大型系统中，可能需要沿着 12 英寸的路径发送 USB 信号。这种长路径可能导致大量损耗，从而严重扭曲数据并导致系统故障。了解有损传输线对于高速数字板和 RF 应用的设计都很有价值。 

有损传输线方程

我们可以按照与无损传输线类似的方法推导出电压和电流方程 。对于有损传输线，复特性阻抗 Z 0 和复传播常数 γ 如下面的公式 1 和公式 2 所示：

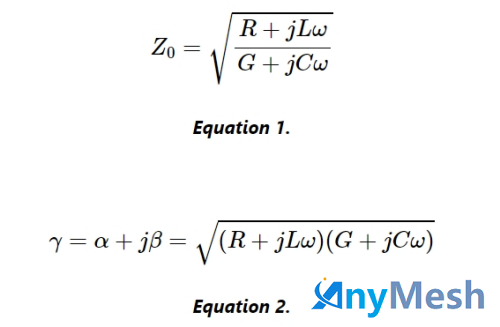
γ 的实部称为衰减常数 ⍺（单位为奈培/米）；虚部称为传播常数 β（单位为弧度/米）。如果该线沿 x 轴，则正向传播的电压波可采用以下形式：

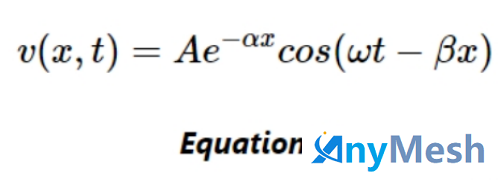
其中 A 是一个常数，可以根据传输线的输入和输出端口的边界条件得出。有损和无损情况之间的一个主要区别是指数项 e-⍺x，它表示信号在沿有损传输线传播时会衰减。为了了解信号上的衰减效应，让我们看一些典型的波形。 

无损传输线VS有损传输线：正弦输入

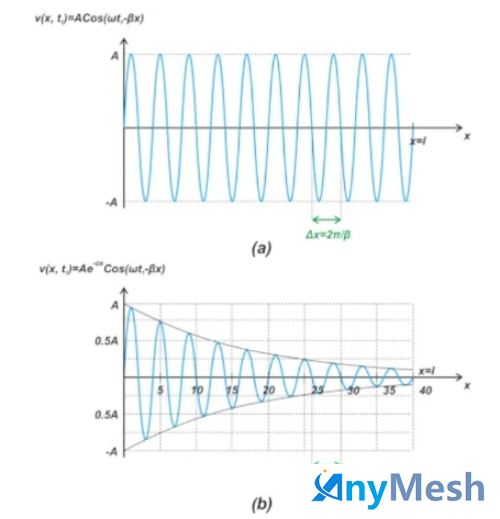
考虑通过 40 英寸长的传输线将源阻抗为 Rs 的正弦输入 Vs cos(⍵t) 施加 到负载阻抗 RL  (下图 (a))。假设没有反射波，前向波由上面公式 3 给出。  

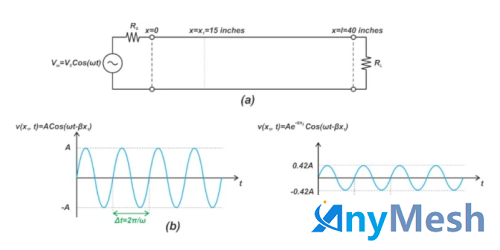
正弦信号通过有损传输线传播

在线上的固定位置 x=x1 处，等式 3 中的 βx 项是恒定相位项，电压方程只是时间的正弦函数。对于无损传输线 (⍺=0)，此正弦函数的振幅是恒定的，无论 x 的值如何都等于 A。因此，在任意位置 x，波形的振幅为 A，如上图 (b) 所示。

然而，对于非零的 ⍺ 值，信号的幅度会沿线减小。例如，如果传输线的损耗为每英寸 0.5 dB，则距离 x1 =15 英寸的总衰减为 7.5 dB。因此，x1 =15 英寸处的电压幅度为：

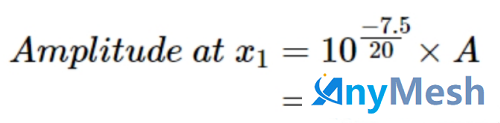
图 (c) 显示了该有损传输线的电压波形AMP=0.42A。现在让我们通过查看特定时刻 t=t1 的波形来检查波形对位置的依赖性。在这种情况下，项 ⍵t 变为恒定相位项。对于无损传输线 (⍺=0)，电压信号变为位置 x 的正弦函数，如下图 (a) 所示。   

无损和有损传输线的正弦信号幅度

在上图 (a) 中，电压电平在线路上的不同点发生变化，但变化幅度是恒定的，并且对于所有 x 值都等于 A。这与图 (b) 中所示的有损情况形成对比。在该图中，假设线路的衰减为 0.5 dB/英寸。当我们远离信号源时，正弦波形的幅度呈指数减小（由于 e-⍺x 项）。请注意，线路衰减随长度线性增加。例如，如果每条线路长度的衰减为 0.1 dB/英寸，则 5 英寸长线路末端的衰减为 0.5 dB。现在要问的问题是，方波会受到有损线路的影响吗？

上面讨论的传输线分别是沿着时间t和沿着传输线距离x的讨论。

有损线路会增加数字信号的上升时间

重要的是要认识到传输线损耗会随着频率的增加而增加。下图显示了使用典型 FR4 基板构建的两个 5 mil 宽 PCB 走线的衰减。该图显示了两条不同线路的衰减与频率的关系：一条长 5 英寸（蓝色），另一条长 10 英寸（红色）。 

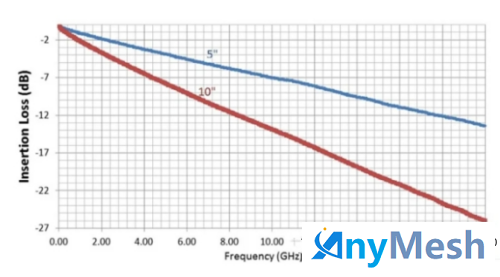
衰减（插入损耗）与频率和走线长度的关系

可以看出，衰减具有低通特性，并且随频率增加而增加。理想情况下，数字信号会从一个逻辑电平突然转换到另一个逻辑电平。时域中的急剧转换对应于频域中的高频分量。例如，上升/下降时间为零的 50% 占空比方波具有其基频的所有奇次谐波。换句话说，上升/下降时间为零的方波具有无限带宽。当此理想方波沿有损传输线传播时，其高频分量不可避免地会因线路的低通特性而衰减。由于这些高频分量被抑制，信号上升/下降时间在沿有损线路传播时会增加。下图显示了信号上升时间沿有损传输线如何增加。 

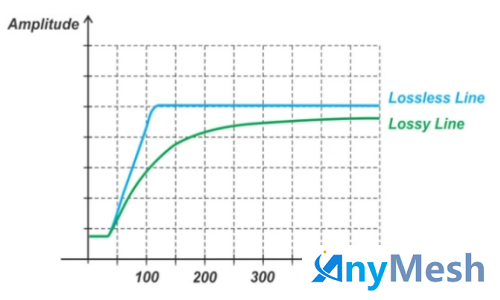
无损和有损传输线的信号上升时间比较

请注意，方波沿线路传播时，其幅度会减小，上升时间会延长。在大多数情况下，上升时间的增加对传输信号的信号完整性的危害比幅度的损失更大。

上升时间恶化导致符号间干扰

下图显示了较长的上升和下降时间如何影响数字系统中的比特流。

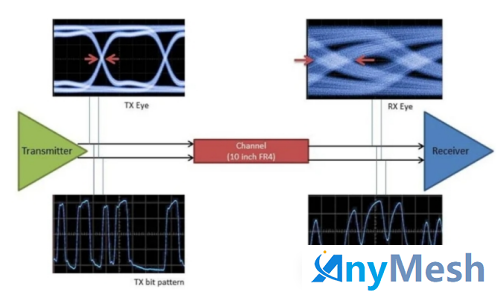
长上升和下降时间对数字信号传输的影响

在发射端，信号转换相对尖锐；然而，当信号到达传输线的远端时，其上升/下降时间会增加。当几个连续的位具有相同的值时，即使上升/下降时间延长，接收信号也可能能够达到其最终值。然而，对于在 1 和 0 之间交替的位流，例如 101010101，传输脉冲的持续时间较短，输出没有足够的时间达到其最终值。因此，给定转换是否达到其最终值取决于bit pattern。 

另请注意，给定转换的最终值是下一个转换的初始值。因此，bit pattern也会影响转换的初始值。这些不良影响会导致数据相关的时序抖动，通常称为符号间干扰 (ISI)。上图还显示了发送和接收信号的眼图。眼图是通过叠加信号的连续波形创建的。请注意失真如何通过闭合的眼图表现出来。下图显示了损耗逐渐增大的传输线对眼图损耗的影响。 

传输线损耗越来越大，数字信号失真也越来越大

左上角的图表是传输的信号。随着 PCB 的 Df 或损耗角正切从零增加到 Df=0.020（对应于典型的 FR4 板），线路的损耗越来越大，眼图张开度也越来越小。正如所见，损耗有两个影响：它会衰减信号并引入失真。失真最终会限制数据速率或需要均衡。

射频系统中的损耗后果 

大多数 RF 系统需要处理小信号。输入信号功率的无意衰减显然是不可取的。信号链中存在有损元件（例如有损传输线）的另一个重要后果是系统噪声系数增加。当损耗为 L 的无源衰减器的物理温度为 T ₀ =290 K 时，其噪声系数为 F=L（或者说，其噪声系数（单位为 dB）等于其损耗（单位为 dB）。例如，假设损耗为 L（以线性而不是分贝表示）的线路位于噪声系数为 F _amp的放大器之前 ，如下图所示。

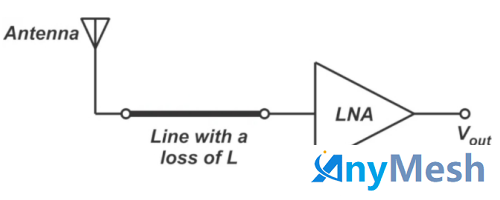
具有有损传输线的 RF 接收器系统

应用 Friis 方程，我们可以发现总体噪声系数为：

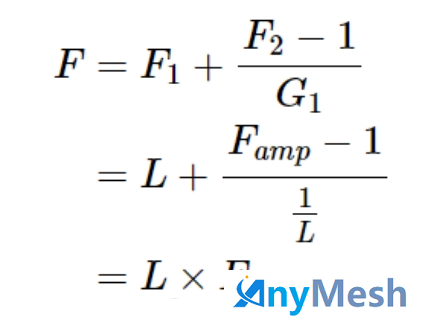
等效地，我们可以用噪声系数值（单位为 dB）来表示上述公式。例如，如果传输线线路损耗为 0.2 dB，放大器噪声系数为 2 dB，则总噪声系数为 2.2 dB。请注意，上述计算基于线路和放大器完全匹配的假设，否则分析可能会更加复杂。在后续文章中，我们可以继续讨论传输线中的不同损耗机制。